Jónsson cardinal

In set theory, a Jónsson cardinal (named after Bjarni Jónsson) is a certain kind of large cardinal number.

An uncountable cardinal number κ is said to be Jónsson if for every function f: [κ]<ω → κ there is a set H of order type κ such that for each n, f restricted to n-element subsets of H omits at least one value in κ.

Every Rowbottom cardinal is Jónsson. By a theorem of Eugene M. Kleinberg, the theories ZFC + “there is a Rowbottom cardinal” and ZFC + “there is a Jónsson cardinal” are equiconsistent. William Mitchell proved, with the help of the Dodd-Jensen core model that the consistency of the existence of a Jónsson cardinal implies the consistency of the existence of a Ramsey cardinal.

In general, Jónsson cardinals need not be large cardinals in the usual sense: they can be singular. But the existence of a singular Jónsson cardinal is equiconsistent to the existence of a measurable cardinal. Using the axiom of choice, a lot of small cardinals (the 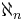\aleph_n, for instance) can be proved to be not Jónsson. Results like this need the axiom of choice, however: The axiom of determinacy does imply that for every positive natural number n, the cardinal 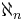\aleph_n is Jónsson.

A Jónsson algebra is an algebra with no proper subalgebras of the same cardinality. (Here an algebra means a model for a language with a countable number of function symbols, in other words a set with a countable number of functions from finite products of the set to itself.) A cardinal is a Jónsson cardinal if and only if there are no Jónsson algebras of that cardinality. The existence of Jónsson functions shows that if algebras are allowed to have infinitary operations, then there are no analogues of Jónsson cardinals.

References